Pembahasan soal Kalkulus Purcell Bab 1 sub bab 4

Makan ketupat di hari Raya
Pembahasan Kalkulus Purcell bab 1 sub bab 4 telah tersedia
Wajah khalifah Ali berseri-serinya
Sangat mohon sekali koreksinya



SOAL-SOAL 1.4

Dalam Soal-soal 1-12, carilah himpunan penyelesaian dari ketaksamaan yang diberikan (lihat Contoh 1 dan 2).
1. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 1
   
2. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 2
   
3. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 3
   
4. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 4
   
5. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 5
   
6. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 6
   
7. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 7
   
8. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 8
   
9. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 9
   
10. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 10
    
11. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 11
    
    
    
    
    
    
    
    
    
    
    
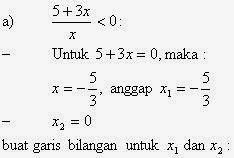
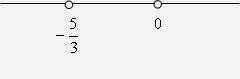
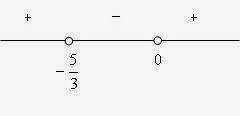
12. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 12
    
    
    
    
    
    
    
    
    
    
    
Dalam Soal-soal 13-16, selesaikan ketaksamaan kuadrat yang diberikan dengan menggunakan rumus kuadrat (lihat Contoh 5)
13. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 13
    
    
    
    
14. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 14
    
    
    
    
15. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 15
    
    
    
    
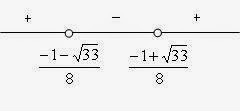
16. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 16
    
    
    
    
Dalam Soal-soal 17-20, buktikan bahwa implikasi yang ditunjukkan adalah benar (lihat Contoh 3).
17. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 17
    
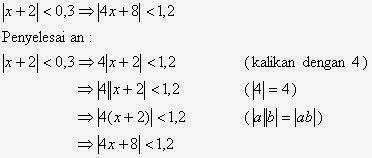
18. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 18
    
19. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 19
    
20. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 20
    
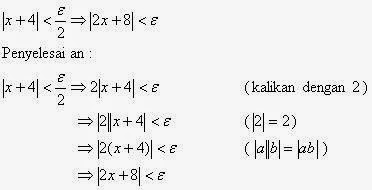Dalam Soal=soal 21-24, carilah (tergantung pada ) sedemikian sehingga implikasi yang diberikan adalah benar (lihat Contoh 4)
21. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 21
    
22. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 22
    
23. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 23
    
24. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 24
    
Dalam Soal-soal 25-28, selesaikanlah ketaksamaan-ketaksamaan tersebut (lihat Contoh 6).
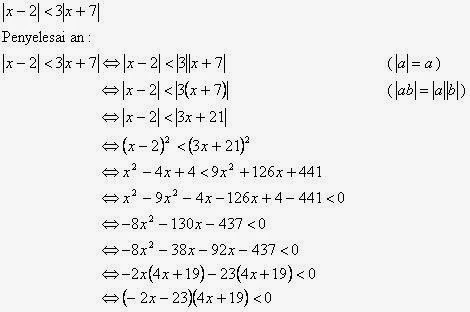
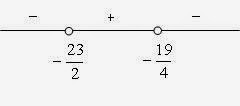
25. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 25
    
    
    
    
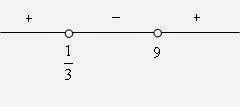
26. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 26
    
    
    
    
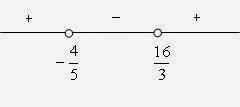
27. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 27
    
    
    
    
28. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 28
    
    
    
    
29. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 29
    
    
    
    
    
    
    Itulah alasan untuk tiap-tiap langkah pembuktiannya, kalau ada yang kurang mengerti silakan ditanya ya.......... ^_^
30. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 30
    Gunakan hasil Soal 29 untuk membuktikan bahwa
    
31. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 31
    Gunakan ketaksamaan segitiga untuk memperlihatkan tiap ketaksamaan berikut.
    
    1. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 31a
       
    2. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 31b
       
    3. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 31c
       
32. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 32
    
    
33. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 33
    
    
34. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 34
    
    
35. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 35
    Buktikan bahwa
    
    menurut ketaksamaan segitiga pada halaman 19:
    
Buktikan masing-masing yang berikut.
36. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 36
    Buktikan masing-masing yang berikut.
    
    
    
    
    
    
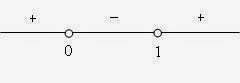
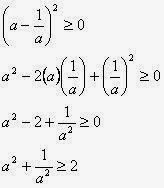
37. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 37
    
    
    
38. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 38
    
39. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 39
    
40. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 40
    
    
    
41. Pembahasan soal Kalkulus Edwin J. Purcell dan Dale Varberg bab 1 sub bab 4 no. 41
    Tunjukkan bahwa di antara semua segi empat dengan keliling p, bujur sangkar memiliki luas paling besar.
    Petunjuk: Bila a dan b merupakan panjang sisi-sisi suatu segi empat dengan keliling p, maka luasnya ab, dan untuk bujur sangkar luasnya adalah
    a²=[(a+b)/2]². Sekarang lihat soal 40.
    Pembahasan:
    Sebagaimana yang kita ketahui, yang termasuk segiempat adalah bujursangkar, persegi panjang, jajargenjang, belahketupat, layang-layang, dan trapesium. Pada petunjuk dikatakan bahwa a dan b adalah sisi-sisi suatu segi empat. Dari semua segi empat yang disebutkan di atas, jika kita misalkan sisi-sisi dari suatu segi empat itu adalah a dan b, maka segi empat yang memiliki luas ab hanyalah bujursangkar dan persegi panjang yang mana pada bujursangkar a sama dengan b. Jadi dapat diambil kesimpulan bahwa segi empat yang dimaksud dalam soal no. 41 ini adalah bujursangkar dan persegi panjang. Jadi yang akan kita buktikan sekarang adalah: “Jika bujur sangkar dan persegi panjang dengan sisi-sisi a dan b memiliki keliling p, maka bujur sangkar mempunyai luas yang lebih besar dibandingkan persegi panjang.
    Cara 1:
    Pada pembahasan soal no. 40 telah terbukti untuk dua bilangan positif a dan b bahwa:
    
    Cara 2:
    Misalkan pada bujur sangkar panjang sisinya adalah c, maka luasnya adalah c². Dan persegi panjang dengan keliling yang sama akan mempunyai ukuran (c+d) dan (c−d) yang mana d tidak sama dengan 0, maka luas persegi panjang adalah (c + d)(c − d) = c²−d². Sudah jelas bahwa c² > c²−d². Jadi terbukti bahwa bujur sangkar yang mempunyai keliling yang sama dengan persegi panjang mempunyai luas yang lebih besar dibanding persegi panjang tersebut.
    

Semoga bermanfaat ya...
by: mans58007@gmail.com
: )

Posted in: