Sistem Basis Bilangan ~ Get Your Dream

Kenapa 8+11 = 19, karena kita bicara di basis 10, Kalau kita bicara di basis 9, maka 11+8=21 (karena tidak ada angka 9 di basis 9), dan bagaimana lagi hasilnya kalau kita bicara di basis 8, basis 7, atau mungkin di basis 2? nanti kita bahas ya...

Sepertinya sudah merupakan kesepakatan internasional kita bicara di basis 10, yaitu sistem bilangan dengan menggunakan sepuluh angka/simbol, karena secara mudah logikanya adalah banyaknya angka yang kita kenal ada sepuluh macam, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9, jadi lebih enak aja berkomunikasi dalam basis 10.

Sebenarnya bahasa komukasi di dunia ini hanyalah sebuah kesepatakan.
Contoh:

7 sudah disepakati menjadi simbol untuk menyatakan jumlah tujuh, sehingga 7 dibaca “tujuh”. Andai saja 8 disepakati menjadi simbol untuk menyatakan jumlah tujuh, sehingga 8 dibaca “tujuh”, maka yang benar adalah 3+4=8 bukan 3+4=7. Dan jika saja # disepakati menjadi simbol untuk menyatakan jumlah tujuh, sehingga # dibaca “tujuh”, maka yang benar adalah 3+4=# bukan 3+4=7
Kenapa warna disebut warna merah? Kenapa tidak hitam atau kuning? Karena memang kesepatakannya seperti itu. Dan kenapa warna disebut warna hijau? Ya karena memang begitu disepakati
Yang kita kenal selama ini hanyalah simbol 9 yang menjadi kesepakatan sebagai satu simbol yang menyatakan jumlah terbanyak (sembilan), artinya untuk menyatakan jumlah yang lebih dari sembilan perlu penggabungan 2 simbol, 10 merupakan penggabungan dari simbol 1 dan 0, dan 33 merupakan penggabungan simbol 3 dengan 3, dan lain sebagainya. Andai saja simbol A disepakati sebagai satu simbol yang menyatakan jumlah sepuluh, maka akan tercipta basis 11, yaitu sistem bilangan yang menggunakan 11 angka/simbol yaitu:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, dan A, dimana:
- 8+2=A adalah pernyataan yang benar dan 8+2=10 adalah pernyataan yang salah
- 10 sekarang sudah merupakan simbol untuk menyatakan jumlah sebelas, dan 11 bukan lagi simbol untuk menyatakan jumlah sebelas, sehingga 8+3=10 adalah pernyataan yang benar dan 8+3=11 adalah pernyataan yang salah, gak bingung kan... ?, janganlah bingung... yang penting cemungut ya... :)

Sebenarnya penulisan yang benar untuk bilangan basis 10 secara berurutan dari
0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9
adalah:
0₁₀, 1₁₀, 2₁₀, 3₁₀, 4₁₀, 5₁₀, 6₁₀, 7₁₀, 8₁₀, 9₁₀, 10₁₀, namun sudah menjadi kesepakatan juga cukup 4₁₀ ditulis 4. Kasusnya sama seperti hal berikut:

cukup ditulis
cukup ditulis log 1000
cukup ditulis ln a
BEGITU JUGA 4₁₀ cukup ditulis 4

Oke kita mulai sistem bilangannya...

Sistem Bilangan Basis 10 (dikenal dengan bilangan desimal)
Sistem bilangan basis 10 merupakan sistem bilangan yang biasa kita pakai dalam kehidupan sehari-hari, sistem bilangan yang menggunakan 10 angka, yaitu:
0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9
Dan penulisannya adalah 0₁₀, 1₁₀, 2₁₀, 3₁₀, 4₁₀, 5₁₀, 6₁₀, 7₁₀, 8₁₀, dan 9₁₀, namun karena sudah kesepakatan cukup ditulis 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9

Rumus bilangan basis 10:

Contoh:
Contoh perhitungan di basis 10:
- 3 + 5 = 8
- 6 - 12 = -7
- 4 x 9 = 36
- 21 / 7 =3
Sistem Bilangan Basis 9
Sistem bilangan basis 9 adalah sistem bilangan yang menggunakan 9 angka, yaitu:
0, 1, 2, 3, 4, 5, 6, 7, dan 8. Dan penulisannya adalah: 0₉, 1₉, 2₉, 3₉, 4₉, 5₉, 6₉, 7₉, dan 8₉
Rumus bilangan basis 9:

Contoh:
- Merubah bilangan 3216₉ ke bentuk bilangan basis 10:
- Merubah bilangan 2365 ke bentuk bilangan basis 9:
  Cari dulu 9 pangkat berapa yang hasilnya besar atau sama dengan 2365, maka didapatlah 94 = 6561, sementara 93 = 729. Jadi 2365 terletak antara 94 dengan 93, maka:
  2365 = ... x 9³ + ... x 9² + ... x 9¹ + ... x 9⁰
  Jika blank pertama diisi dengan angka 4, maka hasilnya akan lebih dari 2365, karena
  4 x 9³ = 2916, dan jika blank pertama diisi dengan angka 3, hasilnya tidak akan lebih 2365, karena
  3 x 9³ = 2187
  Jadi didapat blank pertama diisi dengan angka 3, sehingga:
  
  2365 = 3 x 9³ + ... x 9² + ... x 9¹ + ... x 9⁰
  Jika blank kedua diisi dengan angka 3 maka hasilnya akan lebih besar dari 2365, karena
  3 x 9³ + 3 x 9² = 2430,
  dan jika blank kedua diisi dengan angka 2, hasilnya tidak akan lebih dari 2365, karena
  3 x 9³ + 2 x 9² = 2349, sehingga:
  
  2365 = 3 x 9² + 2 x 9¹ + ... 9⁰
  Dengan cara yang sama seperti sebelumnya didapat bahwa:
  2365 = 3 x 9³ + 2 x 9² + 1 x 9¹ + 7 x 9⁰
  Jadi 2365 di basis 10 sama dengan 3217 di basis 9, atau ditulis 2365 = 3217₉
Sistem Bilangan Basis 8 (dikenal dengan bilangan octal)
Sistem bilangan basis 8 adalah sistem bilangan yang menggunakan 8 angka, yaitu:
0, 1, 2, 3, 4, 5, 6, dan 7
Dan penulisannya adalah:
0₈, 1₈, 2₈, 3₈, 4₈, 5₈, 6₈, 7₈
Rumus bilangan basis 8 adalah:

Contoh:
- Merubah bilangan 5231₈ ke bentuk bilangan basis 10
- Merubah bilangan 2713 ke bentuk bilangan basis 8
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat:
Sistem Bilangan Basis 7 (septenary)
Sistem bilangan basis 7 adalah sistem bilangan yang menggunakan 7 angka, yaitu:
0, 1, 2, 3, 4, 5, dan 6.
Dan penulisannya adalah 0₇, 1₇, 2₇, 3₇, 4₇, 5₇, dan 6₇
Rumus bilangan basis 7:

Contoh:
- Merubah bilangan 1000₇ ke bentuk bilangan basis 10
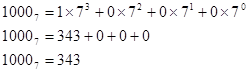
- Merubah bilangan 343 ke bentuk bilangan basis 7
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat:
Sistem Bilangan Basis 6 (senary)
Sistem bilangan basis 6 adalah sistem bilangan yang menggunakan 6 angka, yaitu:
0, 1, 2, 3, 4, dan 5.
Dan penulisannya adalah 0₆, 1₆, 2₆, 3₆, 4₆, dan 5₆
Rumus bilangan basis 6:

Contoh:
- Merubah bilangan 3001₆ ke bentuk bilangan basis 10
- Merubah bilangan 649 ke bentuk bilangan basis 6
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat:
Sistem Bilangan Basis 5 (quinary)
Sistem bilangan basis 5 adalah sistem bilangan yang menggunakan 5 angka, yaitu:
0, 1, 2, 3, dan 4.
Dan penulisannya adalah 0₅, 1₅, 2₅, 3₅, dan 4₅
Rumus bilangan basis 5:

Contoh:
- Merubah bilangan 1234₅ ke bentuk bilangan basis 10
- Merubah bilangan 194 ke bentuk bilangan basis 5
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat:
Sistem Bilangan Basis 4 (dikenal dengan bilangan kuarterner/quaternary)
Sistem bilangan basis 4 adalah sistem bilangan yang menggunakan 4 angka, yaitu:
0, 1, 2, dan 3.
Dan penulisannya adalah 0₄, 1₄, 2₄, dan 3₄
Rumus bilangan basis 4:

Contoh:
- Merubah bilangan 2333₄ ke bentuk bilangan basis 10
- Merubah bilangan 191 ke bentuk bilangan basis 4
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat:
Sistem Bilangan Basis 3 (dikenal dengan bilangan terner/ternery)
Sistem bilangan basis 3 adalah sistem bilangan yang menggunakan 3 angka, yaitu:
0, 1, dan 2.
Dan penulisannya adalah 0₃, 1₃, dan 2₃. Rumus bilangan basis 3:

Contoh:
- Merubah bilangan 1212₃ ke bentuk bilangan basis 10
- Merubah bilangan 50 ke bentuk bilangan basis 3
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat:
Sistem Bilangan Basis 2 (dikenal dengan bilangan biner/biner)
Sistem bilangan basis 2 adalah sistem bilangan yang menggunakan 2 angka, yaitu:
0 dan 1.
Dan penulisannya adalah 0₂ dan 1₂
Rumus bilangan basis 2:

Contoh:
- Merubah bilangan 10100₂ ke bentuk bilangan basis 10
- Merubah bilangan 20 ke bentuk bilangan basis 2
  Dengan menggunakan cara yang sama seperti mengubah bilangan basis 10 ke basis 9 maka didapat: