Jika suatu pertanyaan diajukan kepada kita "Siapakah orang yang paling Anda sayangi?" maka jawabannya beraneka ragam, ada yang bilang pacarnya, ada yang menjawab Ibu, ada yang mengemukakan adiknya, ada yang mengatakan anaknya, Ayah, anak yatim, orang tua renta dan banyak lagi jawaban lain yang mungkin, tapi jika dikumpulkan data dari suatu populasi, maka tentu sangat banyak yang menjawab bahwa orang yang paling disayangi adalah Ibu yang telah melahirkan dan membesarkan kita.
Ya, pasti, karena Ibu adalah wanita yang telah banyak bekorban untuk seorang anaknya, mulai dari masa mengandung yang sangat melelahkan, bayangkan lebih kurang sembilan bulan Ibu kita selalu membawa suatu beban yang beratnya sampai 20 kg kemanapun Ia pergi, tidur dibawa, ke kamar mandi dibawa, ke pasar dibawa, kemanapun Ibu kita pergi. itu baru satu alasan dari sekian banyak alasan, belum lagi rasa mual, letih dan tidak ada nafsu makan yang muncul saat hamil, jika itu kita bayangkan mungkin akan berurai air mata mengingat belum terbalas jasa Ibu. Kemudian lagi sakit apa sih yang paling dahsyat sakitnya selain dari pada SAKIT PADA SAAT MELAHIRKAN? tentu tidak ada, karena sakit pada saat melahirkan adalaha perjuangan seorang Ibu antara hidup dan mati, sehingga tidak sia-sia Nabi kita Muhammad SAW mengatakan dalam haditsnya bahwa wanita yang meninggal dunia saat melahirkan adalah mati syahid, subhanallah. Ya Allah, wahai temanku belum lagi rasa letih pasca melahirkan, menyusui kita. Dan ada juga orang yang mengatakan bahwa "Kasih Ibu Sepanjang Jalan", tak ada putus-putusnya.
SOAL-SOAL 1.5________________________________________________________________________________
Ya, pasti, karena Ibu adalah wanita yang telah banyak bekorban untuk seorang anaknya, mulai dari masa mengandung yang sangat melelahkan, bayangkan lebih kurang sembilan bulan Ibu kita selalu membawa suatu beban yang beratnya sampai 20 kg kemanapun Ia pergi, tidur dibawa, ke kamar mandi dibawa, ke pasar dibawa, kemanapun Ibu kita pergi. itu baru satu alasan dari sekian banyak alasan, belum lagi rasa mual, letih dan tidak ada nafsu makan yang muncul saat hamil, jika itu kita bayangkan mungkin akan berurai air mata mengingat belum terbalas jasa Ibu. Kemudian lagi sakit apa sih yang paling dahsyat sakitnya selain dari pada SAKIT PADA SAAT MELAHIRKAN? tentu tidak ada, karena sakit pada saat melahirkan adalaha perjuangan seorang Ibu antara hidup dan mati, sehingga tidak sia-sia Nabi kita Muhammad SAW mengatakan dalam haditsnya bahwa wanita yang meninggal dunia saat melahirkan adalah mati syahid, subhanallah. Ya Allah, wahai temanku belum lagi rasa letih pasca melahirkan, menyusui kita. Dan ada juga orang yang mengatakan bahwa "Kasih Ibu Sepanjang Jalan", tak ada putus-putusnya.
Tak salah Rasulullah mengatakan bahwa orang yang paling pertama dihormati adalah Ibu kita, setelah itu Ibu kita, setelah itu Ibu kita, dan setelah itu barulah Ayah kita. Jadi derajat Ibu 3 tingkat lebih tinggi dari derajat Ayah. Begitu besar pengorbanan Ibu terhadap kita anaknya, masih sanggupkah kita melalaikan panggilan Ibu kita? Teman..., jika Ibumu memanggilmu, berlarilah segera untuk menemui Ibumu (sekilas dari sahabat).
Berikut pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5, untuk mendownload file .doc (file microsoft word) dari postingan ini silakan baca pada bagian akhir. Mohon koreksi jika ada kesalahan, jika ada yang kurang mengerti silakan ditanya.
Berikut pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5, untuk mendownload file .doc (file microsoft word) dari postingan ini silakan baca pada bagian akhir. Mohon koreksi jika ada kesalahan, jika ada yang kurang mengerti silakan ditanya.
- Dalam Soaal-soal 1-6, rajahlah titik-titik yang diberikan dalam bidang koordinat dan kemudian carilah jarak antara titik-titik tersebut.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 1
(2,-1), (5,3)
Penyelesaian: by: sahabat-informasi.com

Berdasarkan uraian yang ada pada halaman 26, disebutkan bahwa rumus untuk mencari jarak dua titik adalah didasarkan pada Teorema Pythagoras, garis yang dihubungkan oleh titik (2,-1) dengan titik (5,3) merupakan garis yang tidak sejajar dengan sumbu x atau sumbu y. Untuk dapat menggunakan Teorema Pythagoras kita akan membuat sebuah segitiga siku-siku dengan menjadikan garis yang dihubungkan oleh titik (2,-1) dengan titik (5,3) sebagai sisi miring, sehingga didapat gambar sebagai berikut:

Jarak kita simbolkan dengan d yang merupakan huruf awal dari kata bahasa Inggris distance yang berarti jarak. Jadi dengan menggunakan Teorema Pythagoras jarak antara titik (2,-1) dengan titik (5,3) adalah:
Jadi jarak antara titik (2,-1) dengan titik (5,3) adalah 5 satuan. - Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 2
(-2,1), (7,13)
Penyelesaian: by: sahabat-informasi.com

Berdasarkan uraian yang ada pada halaman 26, disebutkan bahwa rumus untuk mencari jarak dua titik adalah didasarkan pada Teorema Pythagoras, garis yang dihubungkan oleh titik (-2,1) dengan titik (7,13) merupakan garis yang tidak sejajar dengan sumbu x atau sumbu y. Untuk dapat menggunakan Teorema Pythagoras kita akan membuat sebuah segitiga siku-siku dengan menjadikan garis yang dihubungkan oleh titik (-2,1) dengan titik (7,13) sebagai sisi miring, sehingga didapat gambar sebagai berikut:

Jarak kita simbolkan dengan d yang merupakan huruf awal dari kata bahasa Inggris distance yang berarti jarak. Jadi dengan menggunakan Teorema Pythagoras jarak antara titik (-2,1) dengan titik (7,13) adalah:
Jadi jarak antara titik (-2,1) dengan titik (7,13) adalah 15 satuan. - Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 3
(4,2), (2,4)
Penyelesaian: by: sahabat-informasi.com

Berdasarkan uraian yang ada pada halaman 26, disebutkan bahwa rumus untuk mencari jarak dua titik adalah didasarkan pada Teorema Pythagoras, garis yang dihubungkan oleh titik (4,2) dengan titik (2,4) merupakan garis yang tidak sejajar dengan sumbu x atau sumbu y. Untuk dapat menggunakan Teorema Pythagoras kita akan membuat sebuah segitiga siku-siku dengan menjadikan garis yang dihubungkan oleh titik (4,2) dengan titik (2,4) sebagai sisi miring, sehingga didapat gambar sebagai berikut:

Jarak kita simbolkan dengan d yang merupakan huruf awal dari kata bahasa Inggris distance yang berarti jarak. Jadi dengan menggunakan Teorema Pythagoras jarak antara titik (4,2) dengan titik (2,4) adalah:
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 4
(-1,5), (6,3)
Penyelesaian: by: sahabat-informasi.com

Berdasarkan uraian yang ada pada halaman 26, disebutkan bahwa rumus untuk mencari jarak dua titik adalah didasarkan pada Teorema Pythagoras, garis yang dihubungkan oleh titik (-1,5) dengan titik (6,3) merupakan garis yang tidak sejajar dengan sumbu x atau sumbu y. Untuk dapat menggunakan Teorema Pythagoras kita akan membuat sebuah segitiga siku-siku dengan menjadikan garis yang dihubungkan oleh titik (-1,5) dengan titik (6,3) sebagai sisi miring, sehingga didapat gambar sebagai berikut:

Jarak kita simbolkan dengan d yang merupakan huruf awal dari kata bahasa Inggris distance yang berarti jarak. Jadi dengan menggunakan Teorema Pythagoras jarak antara titik (-1,5) dengan titik (6,3) adalah:
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 5


Jarak kita simbolkan dengan d yang merupakan huruf awal dari kata bahasa Inggris distance yang berarti jarak.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 6
(2,71;- 3,42), (5,16;4,33)
Penyelesaian: by: sahabat-informasi.com

Berdasarkan uraian yang ada pada halaman 26, disebutkan bahwa rumus untuk mencari jarak dua titik adalah didasarkan pada Teorema Pythagoras, garis yang dihubungkan oleh titik (2,71;- 3,42) dengan titik (5,16;4,33) merupakan garis yang tidak sejajar dengan sumbu x atau sumbu y. Untuk dapat menggunakan Teorema Pythagoras kita akan membuat sebuah segitiga siku-siku dengan menjadikan garis yang dihubungkan oleh titik (2,71;- 3,42) dengan titik (5,16;4,33) sebagai sisi miring, sehingga didapat gambar sebagai berikut:

Jarak kita simbolkan dengan d yang merupakan huruf awal dari kata bahasa Inggris distance yang berarti jarak. Jadi dengan menggunakan Teorema Pythagoras jarak antara titik (2,71;- 3,42) dengan titik (5,16;4,33) adalah:
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 7
Buktikan bahwa segitiga yang titik-titik sudutnya adalah (5,3), (-2,4), dan (10,8) adalah sama kaki!
Penyelesaian: by: sahabat-informasi.com
Segitiga sama kaki adalah segitiga yang mempunyai dua sisi yang sama panjang, sementara sisi yang satunya lagi mempunyai panjang yang berbeda dengan dua sisi yang sama panjang tadi. Jadi ada tiga poin yang akan kita uji, yaitu:
- Apakah garis yang dihubungkan oleh titik (5,3) dengan titik (-2,4) sama panjang dengan garis yang dihubungkan oleh titik (5,3) dengan titik (10,8)? Jika ini terbukti akan diperiksa lagi apakah panjang salah satu garis tersebut berbeda dengan panjang garis yang dihubungkan oleh titik (-2,4) dengan titik (10,8)? Jika iya, maka terbukti bahwa segitiga yang titik-titik sudutnya adalah (5,3), (-2,4), dan (10,8) adalah sama kaki, jika tidak kita lanjut untuk menguji poin ke-2.
- 2. Apakah garis yang dihubungkan oleh titik (-2,4) dengan titik (5,3) sama panjang dengan garis yang dihubungkan oleh titik (-2,4) dengan titik (10,8)? Jika ini terbukti akan diperiksa lagi apakah panjang salah satu garis tersebut berbeda dengan panjang garis yang dihubungkan oleh titik (5,4) dengan titik (10,8)? Jika iya, maka terbukti bahwa segitiga yang titik-titik sudutnya adalah (5,3), (-2,4), dan (10,8) adalah sama kaki, jika tidak kita lanjut untuk menguji poin ke-3.
- 3. Apakah garis yang dihubungkan oleh titik (10,8) dengan titik (5,3) sama panjang dengan garis yang dihubungkan oleh titik (10,8) dengan titik (-2,4)? Jika ini terbukti akan diperiksa lagi apakah panjang salah satu garis tersebut berbeda dengan panjang garis yang dihubungkan oleh titik (5,3) dengan titik (-2,4)? Jika iya, maka terbukti bahwa segitiga yang titik-titik sudutnya adalah (5,3), (-2,4), dan (10,8) adalah sama kaki.
Misalkan l2 adalah panjang garis yang dihubungkan oleh titik (5,3) dengan titik (10,8), maka:
Misalkan l3 adalah panjang garis yang dihubungkan oleh titik (-2,4) dengan titik (10,8), maka:
Dari uraian di atas didapat bahwa l1 sama panjang dengan l2, sementara l3 tidak sama panjang dengan l1 atau l2, maka sudah terbukti bahwa segitiga yang titik-titik sudutnya adalah (5,3), (-2,4), dan (10,8) adalah sama kaki, sehingga kita tidak perlu lagi untuk melakukan pengujian terhadap poin 2 dan 3. - Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 8
Tunjukkan bahwa segitiga yang titik-titik sudutnya adalah (2,-4), (4,0), dan (8,-2) adalah segitiga siku-siku!
Penyelesaian: by: sahabat-informasi.com
Kita tahu bahwa segitiga siku-siku adalah segitiga yang mana kuadrat sisi miringnya sama dengan jumlah kuadrat kedua sisi lainnya, misalkan l1 adalah panjang garis yang dihubungkan oleh titik (2,-4) dengan titik (4,0), l2 adalah panjang garis yang dihubungkan oleh titik (2,-4) dengan titik (8,-2), dan l3 adalah panjang garis yang dihubungkan oleh titik (4,0) dengan titik (8,-2), maka akan dilakukan pengujian terhadap 3 poin berikut:
- Apakah l12 = l22 + l32, jika iya maka terbukti bahwa segitiga yang titik-titik sudutnya (2,-4), (4,0), dan (8,-2) adalah segitiga siku-siku, jika tidak lakukan pengujian terhadap poin 2.
- Apakah l22 = l12 + l32, jika iya maka terbukti bahwa segitiga yang titik-titik sudutnya (2,-4), (4,0), dan (8,-2) adalah segitiga siku-siku, jika tidak lakukan pengujian terhadap poin 3.
- Apakah l32 = l12 + l22, jika iya maka terbukti bahwa segitiga yang titik-titik sudutnya (2,-4), (4,0), dan (8,-2) adalah segitiga siku-siku, jika tidak maka segitiga yang titik-titik sudutnya (2,-4), (4,0), dan (8,-2) bukan merupakan segitiga siku-siku.
l1 adalah panjang garis yang dihubungkan oleh titik (2,-4) dengan titik (4,0), maka:
l2 adalah panjang garis yang dihubungkan oleh titik (2,-4) dengan titik (8,-2)
l3 adalah panjang garis yang dihubungkan oleh titik (4,0) dengan titik (8,-2)
Selanjutnya kita akan melakukan pengujian untuk tiga poin di atas:
- l12 = 20, l22 = 40, dan l32 = 20, l22 + l32 = 60, tidak terpenuhi untuk l12 = l22 + l32, maka kita lanjut ke poin 2
- l12 = 20, l22 = 40, dan l32 = 20, l12 + l32 = 40, terpenuhi bahwa l22 = l12 + l32, maka sudah terbukti bahwa segitiga yang titik-titik sudutnya (2,-4), (4,0), dan (8,-2) adalah segitiga siku-siku, dan tidak perlu lagi kita lakukan pengujian terhadap poin 3.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 9
Titik-titik (3,-1) dan (3,3) adalah titik-titik sudut suatu bujur sangkar. Berikan tiga pasang titik-titik sudut lain yang mungkin.
Penyelesaian: by: sahabat-informasi.com
Akan lebih mudah jika kita membuat gambarnya terlebih dahulu dalam sisitem koordinat.

Misalkan 2 titik tersebut kita beri nama masing-masing dengan A dan B, jarak titik A dengan B adalah:
Jika A dan B merupakan titik-titik sudut yang saling bersebelahan pada sebuah bujur sangkar, maka ada 2 pasang titik sudut yang bisa menjadi titik-titik sudut lainnya pada bujur sangkar tersebut, yaitu:
- Dengan cara menggeser 4 satuan untuk masing-masing titik tersebut ke arah sumbu x negatif dan sejajar dengan sumbu x. Untuk titik (3,-1) jika digeser 4 satuan ke arah sumbu x negatif dan sejajar dengan sumbu x, maka didapat titik (3-4,-1) atau (-1,-1), dan untuk titik (3,3) jika digeser 4 satuan ke arah sumbu x negatif dan sejajar dengan sumbu x, maka didapat titik (3-4,3) atau (-1,3), sehingga titik (-1,-1) dan titik (-1,3) dapat menjadi titik-titik sudut lainnya untuk bujur sangkar tersebut.

- Dengan cara menggeser 4 satuan untuk masing-masing titik tersebut ke arah sumbu x posistif dan sejajar dengan sumbu x. Untuk titik (3,-1) jika digeser 4 satuan ke arah sumbu x positif dan sejajar dengan sumbu x, maka didapat titik (3+4,-1) atau (7,-1), dan untuk titik (3,3) jika digeser 4 satuan ke arah sumbu x positif dan sejajar dengan sumbu x, maka didapat titik (3+4,3) atau (7,3), sehingga titik (7,-1) dan titik (7,3) dapat menjadi titik-titik sudut lainnya untuk bujur sangkar tersebut.


Memang sedikit berbeda dengan 2 pasang titik sebelumnya, sebab luas bujur sangkar dengan menggunakan pasang titik sudut ini lebih kecil dibandingkan dengan luas bujur sangkar dengan menggunakan 2 pasang titik sudut sebelumnya.
Jadi 3 pasang titik sudut lainnya untuk bujur sangkar yang mempunya titik sudut (3,-1) dan (3,3) adalah:
- Titik (-1,-1) dan titik (-1,3)
- Titik (7,-1) dan titik (7,3)
- Titik (1,1) dan titik (5,1)
- Dengan cara menggeser 4 satuan untuk masing-masing titik tersebut ke arah sumbu x negatif dan sejajar dengan sumbu x. Untuk titik (3,-1) jika digeser 4 satuan ke arah sumbu x negatif dan sejajar dengan sumbu x, maka didapat titik (3-4,-1) atau (-1,-1), dan untuk titik (3,3) jika digeser 4 satuan ke arah sumbu x negatif dan sejajar dengan sumbu x, maka didapat titik (3-4,3) atau (-1,3), sehingga titik (-1,-1) dan titik (-1,3) dapat menjadi titik-titik sudut lainnya untuk bujur sangkar tersebut.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 10
Carilah titik pada sumbu x- yang berjarak sama dari (3,1) dan (6,4)
Penyelesaian: by: sahabat-informasi.com
Misalkan:
titik (3,1) dianggap sebagai titik A, x1 = 3 dan y1 = 1,
titik (6,4) dianggap sebagai titik B, x2 = 6 dan y2 = 4,
titik yang akan dicari pada sumbu x dianggap sebagai titik C (x3, y3), karena titik C berada di sumbu x, maka y3 = 0, sehingga koordinat titik C = (x3, 0)
jarak titik C ke titik A = jarak titik C ke titik B, maka:
Dari uraian di atas didapat x3 = 7, berarti koordinat titik C = (7,0). Jadi titik yang berjarak sama dari titik (3,1) dan titik (6,4) adalah (7,0) - Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 11
Tentukan jarak antara (-2,3) dengan titik tengah potongan garis yang digabungkan (-2,-2) dan (4,3)
Penyelesaian: by: sahabat-informasi.com
Terlebih dahulu kita akan mencari titik tengah dari garis yang digabungkan oleh titik (-2,-2) dengan titik (4,3).
Untuk mencari absis (koordinat x) dari titik tengah garis yang digabungkan oleh titik (-2,-2) dengan titik (4,3), kita mencari nilai tengah dari absis dari kedua titik tersebut, absis dari kedua titik tersebut adalah -2 dan 4, dan nilai tengah dari -2 dan 4 adalah (-2+4)/2 = 1
Untuk mencari ordinat (koordinat y) dari titik tengah garis yang digabungkan oleh titik (-2,-2) dengan titik (4,3), kita mencari nilai tengah dari ordinat kedua titik tersebut, ordinat dari kedua titik tersebut adalah -2 dan 3, dan nilai tengah dari -2 dan 3 adalah (-2+3)/2 = ½.
Jadi koordinat dari titik tengah garis yang digabungkan oleh titik (-2,-2) dengan titik (4,3) adalah (1,½). Setelah itu baru kita akan mencari jarak titik (-2,3) dengan (1,½). Dengan menggunakan rumus jarak maka jarak titik (-2,3) dengan titik (1,½) adalah:
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 12
Carilah panjang ruas garis yang menghubungkan titik-titik tengah ruas-ruas AB dan CD, di mana A = (1,3), B = (2,6), C = (4,7), dan D = (3,4)
Penyelesaian: by: sahabat-informasi.com
Kita akan mencari dulu titik tengah AB dan CD. Misalkan titik tengah AB adalah E, dan titik tengah CD adalah F.
Mencari korrdinat titik E,
xE = ½ (xA + xB) = ½ (1 + 2) = ½ (3) = 3/2;
yE = ½ (yA + yB) = ½ (3 + 6) = ½ (9) = 9/2
didapat koordinat titik E = (3/2 , 9/2)
Mencari koordinat titik F,
xF = ½ (xC + xD) = ½ (4 + 3) = ½ (7) = 7/2
yF = ½ (yC + yD) = ½ (7 + 4) = ½ (11) =11/2
didapat koordinat titik F = (7/2 , 11/2)
sekarang kita akan mencari jarak antara titik E dengan titik F yang merupakan panjang ruas garis yang menghubungkan titik-titik tengah ruas-ruas AB dan CD.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 13
Pusat (1,-2), jari-jari 6.
Penyelesaian: by: sahabat-informasi.com
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
Maka persamaan lingkaran berjari-jari 6 dan pusat (1,-2) adalah:
(x – 1)2 + (y + 2)2 = 62
(x – 1)2 + (y + 2)2 = 36
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 14
Pusat (-3,4), jari-jari 8.
Penyelesaian: by: sahabat-informasi.com
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
Maka persamaan lingkaran berjari-jari 8 dan pusat (-3,4) adalah:
(x + 3)2 + (y - 4)2 = 82
(x + 3)2 + (y - 4)2 = 64
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 15
Pusat (2,-1), melalui (5,3).
Penyelesaian: by: sahabat-informasi.com
Pada soal ini tidak diketahui berapa panjang jari-jari lingkaran, tapi diketahui bahwa lingkaran tersebut melalui titik (5,3), berarti jari-jari lingkaran ini adalah jarak dari titik pusat (2,-1) ke titik (5,3).
Didapat jarak dari titik pusat (2,-1) ke sebuah titik yang dilalui oleh lingkaran tersebut, titik (5,3) adalah 5 satuan, berarti jari-jari lingkaran tersebut adalah 5 satuan.
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
Maka persamaan lingkaran berjari-jari 5 dan pusat (2,-1) adalah:
(x - 2)2 + (y + 1)2 = 52
(x - 2)2 + (y + 1)2 = 25
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 16
Pusat (4,3), melalui (6,2).
Penyelesaian: by: sahabat-informasi.com
Pada soal ini tidak diketahui berapa panjang jari-jari lingkaran, tapi diketahui bahwa lingkaran tersebut melalui titik (6,2), berarti jari-jari lingkaran ini adalah jarak dari titik pusat (4,3) ke titik (6,2).
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 17
Garis tengah AB, dengan A = (-1,2) dan B = (3,8)
Penyelesaian: by: sahabat-informasi.com
Garis tengah adalah sebutan lain untuk diameter, jadi diameter lingkaran itu adalah AB, maka, pusat lingkaran adalah titik di tengah garis AB, kita misalkan titik tengah AB adalah C, akan kita cari terlebih dahulu koordinat dari titik C.
xC = ½ (xA + xB) = ½ (-1 + 3) = ½ (2) = 1
yC = ½ (yA + yB) = ½ (2 + 8) = ½ (10) = 5
didapat koordinat titik C = (1,5).
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 18
Pusat (3,4) dan menyinggung sumbu x.
Penyelesaian: by: sahabat-informasi.com
Lingkaran berpusat di (3,4), karena lingkaran sumbu x, maka titi singgung lingkaran dengan bumbu x adalah (3,0), berarti jari-jari lingkaran adalah jarak dari titik pusat (3,4) ke salah satu titik di tepi lingkaran (3,0), yaitu 4 satuan, atau kalau ingin gunakan rumus jarak juga bisa:
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
Maka persamaan lingkaran berjari-jari 4 dan pusat (3,4) adalah:
(x - 3)2 + (y - 4)2 = 42
(x - 3)2 + (y - 4)2 = 16
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 19
Cari koordinat y dari dua titik pada lingkaran dari Soal 13 dengan koordinat x adalah 3 (lihat Contoh 2)
Penyelesaian: by: sahabat-informasi.com
Pada pembahasan soal nomor 13 sudah didapat bahwa persamaan lingkarannya adalah:
(x – 1)2 + (y + 2)2 = 36, jika x = 3, maka:
(3 – 1)2 + (y + 2)2 = 36
22 + (y + 2)2 = 36
4 + y2 + 4y + 4 = 36
y2 + 4y + 8 – 36 = 0
y2 + 4y – 28 = 0,
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 20
Cari koordinat x dari dua titik pada lingkaran dari Soal 14 dengan koordinat y adalah 8.
Penyelesaian: by: sahabat-informasi.com
Pada pembahasan soal nomor 14 sudah didapat bahwa persamaan lingkarannya adalah:
(x + 3)2 + (y - 4)2 = 64, jika y = 8 maka:
(x + 3)2 + (8 - 4)2 = 64
(x + 3)2 + (4)2 = 64
(x + 3)2 + 16 = 64
(x + 3)2 = 64 – 16
(x + 3)2 = 48
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 21
x2 + y2 + 2x – 10y + 25 = 0
Penyelesaian: by: sahabat-informasi.com
Sehingga, x2 + y2 + 2x – 10y + 25 = 0 dapat kita uraikan menjadi:
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2, berarti pusat lingkaran tersebut adalah (-1,5) dengan jari-jari 1
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 22
x2 + y2 – 6y = 16
Penyelesaian: by: sahabat-informasi.com
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2, berarti pusat lingkaran tersebut adalah (0,3) dengan jari-jari 5
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 23
x2 + y2 - 12x + 35 = 0
Penyelesaian: by: sahabat-informasi.com
Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2, berarti pusat lingkaran tersebut adalah (6,0) dengan jari-jari 1
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 24
x2 + y2 – 10x + 10y = 0
Penyelesaian: by: sahabat-informasi.com
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 25
4x2 + 4y2 + 4x – 12y +1 = 0
Penyelesaian: by: sahabat-informasi.com
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 26
SOALNYA KELUPAAN
Penyelesaian: by: sahabat-informasi.com
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 27
Titik-titik (2,3), (6,3), (6,-1), dan (2,-1) adalah sudut-sudut suatu bujursangkar. Carilah persamaan-persamaan lingkaran dalam dan lingkaran luar.
Penyelesaian: by: sahabat-informasi.com
- Persamaan lingkaran dalam bujursangkar

Pertama kita akan mencari titik pusat dari lingkaran dalam bujursangkar. Karena keempat sisi bujur sangkar bersingggungan dengan lingkaran, maka tentu titik pusat lingkaran sama dengan titik pusat bujur sangkar tersebut. Dari gambar tampak bahwa koordinat titik pusat bujur sangkar tersebut adalah (4,1), atau jika kita cari dengan memanfaatkan titik-titik sudut bujursangkar didapat:
Koordinat x = ½ (2+6) = ½ (8) = 4
Koordinat y = ½ (-1+3) = ½ (2) = 1
Jadi koordinat titik pusat bujursangkar tersebut adalah (4,1), maka koordinat titik pusat lingkaran juga (4,1)
Kemudian kita akan mencari jari-jari dari lingkaran tersebut. Karena lingkaran berada di dalam bujursangkar, tentu jari-jari lingkaran sama dengan jarak titik pusat lingkaran ke titik singgung lingkaran dengan bujursangkar. Karena sisi-sisi bujursangkar ada yang sejajar dengan sumbu x, maka salah satu titik singgung lingkaran dengan bujursangkar tersebut dapat dicari dengan menarik garis lurus sejajar sumbu x dari pusat lingkaran ke kiri atau ke kanan sampai menyentuh sisi bujursangkar dengan batasan garis x = 2 untuk sisi kiri bujursangkar dan garis x = 6 untuk sisi kanan bujursangkar.
Misalkan kita tarik garis lurus sejajar sumbu x dari titik pusat lingkaran (4,1) ke kiri sisi bujursangkar, maka akan didapat koordinat titik singgung lingkaran dengan bujur sangkar dengan koordinat x = 2 (sesuai dengan batasan garis x = 2) dan koordinat y = 1 (karena garis yang ditarik sejajar dengan sumbu x, sehingga tidak merubah untuk koordinat y). Jadi salah satu titik singgung lingkaran dengan bujur sangkar tersebut adalah titik (2,1), sehingga jari-jari lingkaran adalah jarak dari titik pusat lingkaran (4,1) ke titik salah satu titik singgung lingkaran dengan bujursangkar (2,1).
Dengan menggunakan Teorema Pythagoras jarak antara titik (4,1) dengan titik (2,1) adalah:
didapat jari-jari lingkaran adalah 2 satuan
Jadi lingkaran tersebut mempunyai jari-jari 2 dengan pusat (4,1). Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2, maka persamaan lingkaran tersebut adalah:
(x - 4)2 + (y - 1)2 = 22 atau (x - 4)2 + (y - 1)2 = 4
- Persamaan lingkaran luar bujursangkar

Pertama kita akan mencari titik pusat dari lingkaran luar bujursangkar. Karena keempat titik sudut bujur sangkar bersingggungan dengan lingkaran, maka tentu titik pusat lingkaran sama dengan titik pusat bujur sangkar tersebut. Dari gambar tampak bahwa koordinat titik pusat bujur sangkat tersebut adalah (4,1), atau jika kita cari dengan memanfaatkan titik-titik sudut bujur sangkar didapat:
Koordinat x = ½ (2+6) = ½ (8) = 4
Koordinat y = ½ (-1+3) = ½ (2) = 1
Jadi koordinat titik pusat bujur sangkar tersebut adalah (4,1), maka koordinat titik lingkaran juga (4,1).
Kemudian kita akan mencari jari-jari dari lingkaran. Karena lingkaran berada di luar bujur sangkar, maka jari-jari lingkaran tersebut sama dengan jarak titik pusat bujur sangkar ke salah satu titik sudut bujur sangakr tersebut. Misalkan kita akan mencari jarak dari titik pusat bujur sangkar (4,1) ke salah satu titik sudut bujur sangkar (2,3).
Dengan menggunakan Teorema Pythagoras jarak antara titik (4,1) dengan titik (2,3) adalah:
- Persamaan lingkaran dalam bujursangkar
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 28
Sebuah tali secara ketat mengelilingi dua lingkaran dengan persamaan (x - 1)2 + (y + 2)2 = 16 dan (x + 9)2 + (y - 10)2 = 16. Berapakah panjang tali ini?
Penyelesaian: by: sahabat-informasi.com
(x - 1)2 + (y + 2)2 = 16 atau (x - 1)2 + (y – (-2))2 = 42 adalah lingkaran dengan titik pusat (1,-2) dengan jari-jari 4 dan (x + 9)2 + (y - 10)2 = 16 atau (x – (-9))2 + (y - 10)2 = 42 adalah lingkaran dengan titik pusat (-9,10) dengan jari-jari 4.

Panjang tali tersebut adalah panjang tali yang melekat pada ½ lingkaran pertama ditambah dengan panjang tali yang melekat pada ½ lingkaran kedua ditambah dengan panjang tali (ada 2) yang menghubungkan kedua lingkaran tersebut.
Jika kita gunakan π = 3,14, maka panjang tali yang melekat pada ½ lingkaran pertama adalah:
½ x (2 π r) = π r = (3,14) (4) = 12,56 satuan
Panjang tali yang melekat pada ½ lingkaran kedua sama dengan panjang tali yang melekat pada ½ lingkaran pertama yaitu 12,56 satuan.
Panjang tali yang menghubungkan kedua lingkaran sama dengan jarak dari titik pusat lingkaran 1 terhadap titik pusat lingkaran 2, dengan menggunakan Teorema Pythagoras jarak antara titik (1,-2) dengan titik (-9,10) adalah:
Jadi panjang tali tersebut seluruhnya adalah = 2 x 12,56 + 2 x 14,629 = 25,12 + 29,257 = 54,37 satuan
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 29
Kota-kota di A, B, dan C merupakan titik-titik sudut sebuah segitiga siku-siku, dengan sudut siku-siku di titik sudut B, AB dan BC juga merupakan jalan, masing-masing dengan panjang 214 dam 179 mil. Sebuah pesawat terbang dapat menerbangi rute AC, yang bukan suatu jalan. Biaya mengirim suatu barang tertentu dengan truk $3,71 tiap mil dan dengan pesawat terbang 4,82 tiap mil. Putuskan apakah lebih murah mengirim barang tersebut dari A ke C dengan truk atau dengan pesawat terbang dan cari biaya total memakai metode yang lebih murah.
Penyelesaian: by: sahabat-informasi.com

Dengan menggunakan teorema phytagoras dapat dicari panjang AC, yaitu:
Panjang lintasan AC = 278,993 mil
Dengan menggunakan truk
Panjang lintasan yang dilalui dengan menggunakan truk adalah: AB + BC = 214 + 179 = 393 mil.
Biaya pengiriman dengan truk = 393 x $3,71 = $1.458,03
Dengan menggunakan pesawat terbang
Panjang lintasan yang dilalui dengan menggunakan pesawat terbang adalah: AC = 278,993 mil
Biaya pengiriman dengan pesawat terbang = 278,993 x $4,82 = $1.344,745
Jadi lebih murah biaya pengiriman barang dari A ke C dengan menggunakan pesawat terbang yaitu $1.344,745
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 30
Kota B berjarak 10 mil ke arah hilir dari kota A dan berseberangan dari sungai yang lebarnya ½ mil. Mary Crane akan lari dari kota A sepanjang sungai sejauh 6 mil, kemudian berenang secara diagonal ke kota B. Jika ia lari dengan kecepatan 8 mil/jam dan berenang dengan kecepatan 3 mil/jam, berapa lama waktu yang ditempuhnya dari kota A ke kota B? Anggap laju arus dapat diabaikan.
Penyelesaian: by: sahabat-informasi.com

Kita misalkan Mary Crane mulai berenang dari titik C, dan lebar sungai kita ambil CD. Karena Mary Crane sudah berlari dari titik A ke titik C sejauh 6 mil, maka tentu panjang lintasan dari titik D ke B adalah 10 – 6 = 4 mil. Dengan menggunakan teorema Phytagoras dapat dicari panjang BC, yaitu:
Waktu yang dibutuhkan Mary Crane untuk berlari dari titik A ke titik C
Ingat kembali rumus keterkaitan jarak (s), waktu (t), dan kecepatan (v):
Waktu yang dibutuhkan Mary Crane untuk berenang dari titik C ke titik B
Total waktu dari kota A ke kota B adalah: 0,75 jam + 1,344 jam = 2,094 jam. Jadi total waktu yang dibutuhkan oleh Mary Crane dari kota A ke kota B adalah sekitar 2,094 jam dengan mengabaikan kecepatan arus.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 31
Buktikan bahwa titik tengah sisi miring sebarang segitiga siku-siku berjarak sama dari ketiga titik-titik sudutnya.
Penyelesaian: by: sahabat-informasi.com
Misalkan kita buat sebuah segitiga siku-siku sebarang seperti pada gambar di bawah ini:

Sisi miring dari segitiga siku-siku tersebut adalah KM, akan kita cari koordinat dari titik tengah sisi KM, kita misalkan titik tengah sisi KM tersebut dengan titik N

Yang akan kita buktikan adalah:- Apakah jarak titik N dengan titik L sama dengan jarak titik N dengan titik K, atau
- Apakah jarak titik N dengan titik L sama dengan jarak titik N dengan titik M
Kita lanjut untuk mencari jarak titik N dengan titik L, menurut rumus jarak, jarak titik N dengan titik L adalah:
Kemudian kita lanjut mencari jarak titik N dengan titik K, menurut rumus jarak, jarak titik N dengan titik K adalah:
Dari uraian di atas didapat bahwa jarak titik N dengan titik L sama dengan jarak titik N dengan titik K, berarti titik N berjarak sama dengan ketiga titik sudut K, L, dan M. Terbukti bahwa jarak titik tengah sisi miring sebuah segitiga siku-siku sebarang berjarak sama dengan ketiga titik sudutnya.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 32
Cari persamaan lingkaran yang melingkupi segitiga siku-siku yang titik-titik sudutnya adalah (0,0), (8,0), dan (0,6).
Penyelesaian: by: sahabat-informasi.com

Lingkaran melingkupi segitiga siku-siku, berarti segitiga siku-siku berada di dalam lingkaran dan ketiga titik sudut segitiga siku-siku tersebut bersinggungan dengan lingkaran. Pada pembahasan soal nomor 31, sudah dibuktikan bahwa titik tengah sisi miring suatu segitiga siku-siku sebarang mempunyai jarak yang sama terhadap ketiga titik sudutnya. Pada kasus soal nomor 32, ketiga titik sudut segitiga siku-siku bersinggungan dengan lingkaran, berarti titik tengah dari sisi miring segitiga siku-siku tersebut mempunyai jarak yang sama terhadap ketiga titik sudutnya yang bersinggungan dengan lingkaran. Bukankah itu merupakan jari-jari lingkaran? Ya, itu adalah jari-jari lingkaran, maka tentu titik tengah dari sisi miring segitiga siku-siku tersebut merupakan titi pusat lingkaran.
Jadi jari-jari lingkaran luar segitiga siku-siku sama dengan jarak titik tengah dari sisi miring segitiga siku-siku tersebut dengan ketiga titik sudutnya.
Mencari koordinat titik tengah dari sisi miring segitiga siku-siku
Kita misalkan titik sudut (0,6) adalah titik A, titik sudut (8,0) adalah titik B, titik sudut (0,0) adalah titik O, dan titik tengah dari sisi miring segitiga siku-siku adalah titik C
Koordinat x = ½ (xA + xB) = ½ (0 + 8) = ½ (8) = 4
Koordinat y = ½ (yA + yB) = ½ (6 + 0) = ½ (6) = 3
Jadi koordinat titik C adalah (4,3)
Mencari jarak titik tengah dari sisi miring segitiga siku-siku dengan salah satu titik sudutnya
Kita akan pakai saja titik sudut O. Menurut rumus jarak, jarak titik C dengan titik O adalah:
Berarti lingkaran tersebut mempunyai jari-jari 5 dengan titik pusat (4,3). Menurut rumus persamaan lingkaran pada halaman 27, lingkaran berjari-jari r dan pusat (h,k) mempunyai persamaan:
(x - h)2 + (y - k)2 = r2,
Maka persamaan lingkaran berjari-jari 5 dan pusat (4,3) adalah:
(x – 4)2 + (y – 3)2 = 52
(x – 4)2 + (y – 3)2 = 25
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 33
Perlihatkan bahwa dua lingkaran x2 + y2 – 4x – 2y – 11 = 0 dan x2 + y2 + 20x – 12y + 72 = 0 tidak berpotongan. Petunjuk: Cari jarak antara pusat-pusatnya
Penyelesaian:
Mencari jari-jari dan titik pusat dari lingkaran x2 + y2 – 4x – 2y – 11 = 0
Penyelesaian: by: sahabat-informasi.com
Mencari jari-jari dan titik pusat dari lingkaran x2 + y2 – 4x – 2y – 11 = 0
Diketahui bahwa x2 + y2 – 4x – 2y – 11 = 0 merupakan lingkaran berjari-jari 4 dengan pusat (2,1)
Mencari jari-jari dan titik pusat dari lingkaran x2 + y2 + 20x – 12y + 72 = 0
Didapat bahwa x2 + y2 + 20x – 12y + 72 = 0 merupakan lingkaran berjari-jari 8 dengan pusat (–10,6)
Mencari jarak antara titik (2,1) dengan titik (–10,6)
Dengan menggunakan rumus jarak maka:
Jarak titik pusat kedua lingkaran adalah 13 satuan, sementara jika kita tarik garis dari titik pusat masing-masing lingkaran yang saling menuju ke lingkaran lainnya sepanjang jari-jarinya masing-masing, total dari panjang kedua garis tersebut hanya 12 satuan, jadi ada jarak 1 satuan antara kedua lingkaran.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 34
Bagaimanakah hubungan antara a, b, dan c yang harus dipenuhi bila a2 + ax + y2 + by + c = 0 merupakan persamaan lingkaran?
Penyelesaian: by: sahabat-informasi.com
Salah satu syarat yang harus dipenuhi oleh suatu persamaan lingkaran adalah mempunyai variabel x2, sementara pada soal nomor 34 ini tidak ada variabel x2nya, maka persamaan tersebut bukanlah persamaan lingkaran, jadi menurut sahabat terjadi kekeliruan dalam penulisan soal yang seharusnya x2 tertulis a2, jadi persamaan yang seharusnya adalah x2 + ax + y2 + by + c = 0.
Kita akan uraikan persamaan tersebut dengan melengkapi kuadrat:
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 35
Tentukan panjang dari tali bersilang pada Gambar 8 yang dipasang erat di sekeliling lingkaran (x – 2)2 + (y – 2)2 = 9 dan (x – 10)2 + (y – 8)2 = 9.
Catatan: Diperlukan sedikit pengertian trigonometri untuk menyelesaikan soal ini.

GAMBAR 8
Penyelesaian: by: sahabat-informasi.com
(x – 2)2 + (y – 2)2 = 9 atau (x – 2)2 + (y – 2)2 = 32 adalah lingkaran berjari-jari 3 dengan pusat pada titik (2,2) dan (x – 10)2 + (y – 8)2 = 9 atau (x – 10)2 + (y – 8)2 = 32 adalah lingkaran berjari-jari 3 dengan pusat pada titik (10,8).
Ingat bahwa garis singgung suatu lingkaran selalu tegak lurus dengan jari-jari lingkaran yang melalui titik singgung tersebut. Misalkan kita membuat suatu jaru-jari yang melalui sebuah titik singgung lingkaran, dan kita beri suatu penamaan titik untuk memperjelas perhitungan seperti gambar berikut:

Kita akan mencari panjang tali yang melekat pada sebuah lingkaran, dengan menggunakan perbandingan sudut juring lingkaran. Untuk lebih jelaskan simak uraian berikut:
Kita akan mencari jarak antara kedua titik pusat lingkaran untuk mengetahui panjang AC. Menurut rumus jarak jarak antara titik (2,2) dengan titik (10,8) adalah:
Didapat jarak antara kedua titik pusat lingkaran 10, sementara titik C berada di tengah kedua titik pusat lingkaran, maka tentu panjang AC adalah ½ dari jarak kedua titik pusat lingkaran atau AC = ½ x 10 = 5.
Sekarang sudah diketahui panjang sisi miring dan sebuah sisi lainnya pada segitiga siku-siku tersebut, tentu bisa diterapkan definisi sinus atau cosinus untuk mencari besar suatu sudut tertentu. Sekarang diketahui panjang AB dan panjang AC, maka tentu bisa didapat besar sudut BAC dengan menggunakan definisi Cosinus.
Perhatikan gambar berikut:

Jika besar sudut BAC adalah sekitar 53,13o, maka besar sudut BAD adalah 2 kali sudut BAC = 2 x 53,13o = 106,26o
Kalau kita perhatikan dengan seksama, jika kita memandang suatu sudut pasti kita menemukan 2 besar sudut yang total keduanya adalah 360o, seperti pada sudut BAD, ada sudut BAD kecil (yang pada gambar kita sudutnya membuka ke kanan) yaitu 106,26o dan ada sudut BAD besar (yang pada gambar kita sudutnya membuka ke kiri) yaitu 360o-106,26o = 253,74o.
Dengan mengetahui besar sudut BAD besar, kita dapat mengetahui panjang tali yang melekat pada satu lingkaran.
Pada segitga siku-siku ABC, panjang BC adalah:
Total panjang tali adalah 2 kali panjang tali yang melekat pada suatu lingkaran + 4 kali panjang BC = 2 x 13,28 + 4 x 4 = 26,558 + 16 = 42,558
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 36
Tunjukkan bahwa himpunan titik-titik yang jaraknya ke (3,4) dua kali lebih besar dari jarak ke (1,1) membentuk suatu lingkaran. Tentukan pusat dan jari-jari lingkaran tersebut.
Penyelesaian: by: sahabat-informasi.com
Kadang kalau dibaca sekilas soal ini, kita belum menangkap apa maskud dari soal, untuk mempermudahkan memahami kalimat soal ini, sahabat akan mengubah atau menambahkan sedikit kalimat pada soal, sehingga kalimat soal kita sekarnag menjadi:
“Tunjukkan bahwa himpunan titik-titik yang jarak himpunan titik-titik tersebut ke (3,4) dua kali lebih besar dari jarak himpunan titik-titik tersebut ke (1,1) membentuk suatu lingkaran. Tentukan pusat dan jari-jari lingkaran tersebut”
Semoga sekarang maksud dari soal sudah dapat dipahami, kita lanjut untuk menyelesaikannya.
Maksud dari soal adalah, misalkan ada suatu titik (x,y), misalkan jarak titik (x,y) dengan (3,4) adalah a, maka jarak titik (x,y) dengan (1,1) adalah 2a.
Menurut rumus jarak jarak titik (x,y) dengan titik (3,4) adalah:
Sekarang jarak titik (x,y) ke (3,4) dua kali lebih besar dari jarak titik (x,y) ke (1,1), maka:
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 37
Teorema Pythagoras menyebutkan bahwa luas A, B dan C dari segi empat-segi empat pada Gambar 9 memenuhi A + B = C. Tunjukkan bahwa setengah lingkaran dan segitiga sama sisi juga memenuhi persamaan tersebut.
Gambar 9:

Penyelesaian: by: sahabat-informasi.com
Misalkan sebuah segitiga siku-siku mempunyai panjang sisi a, b, dan c seperti gambar di bawah ini:

Menurut teorema Phytagoras,
c2 = a2 + b2
kita juga dapat mengatakan bahwa:
c2 adalah luas sebuah bujur sangkar dengan panjang sisi c
a2 adalah luas sebuah bujur sangkar dengan panjang sisi a
b2 adalah luas sebuah bujur sangkar dengan panjang sisi b
Misalkan C = c2, A = a2, dan B = b2, maka:
C = A + B

C = A + B
Untuk 3 buah ½ lingkaran dengan diameter dari lingkaran tersebut adalah sisi-sisi sebuah segitiga siku-siku
Suatu ½ lingkaran dengan diameter d akan mempunyai luas:
sehingga:
Menurut teorema Phytagoras pada gambar segitiga siku-siku di atas:
Terbukti bahwa luas ½ lingkaran dengan diameter sisi miring sebuah segitiga siku-siku sama dengan luas ½ lingkaran dengan diameter sisi siku-siku sebuah segitiga siku-siku yang sama ditambah dengan luas ½ lingkaran dengan diameter sisi siku-siku lainnya pada sebuah segitiga siku-siku yang sama.

C = A + B
Untuk 3 buah segitiga sama sisi dengan panjang sisi ketiga segitiga sama sisi tersebut adalah sisi-sisi sebuah segitiga siku-siku

Ingat kembali cara mencari luas segitiga sama sisi!

Menurut teorema Phytagoras pada segitiga siku-siku di atas:
Terbukti bahwa luas segitiga sama sisi dengan panjang sisinya sisi miring sebuah segitiga siku-siku sama dengan luas segitiga sama sisi dengan panjang sisinya salah satu sisi siku-siku sebuah segitiga siku-siku yang sama ditambah dengan luas segitga sama sisi dengan panjang sisinya sisi siku-siku lainnya pada sebuah segitga siku-siku yang sama.
- Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 38
Diketahui sebuah lingkaran C dan sebuah titik P yang berada di luar lingkaran tersebut. Apabila potongan garis PT menyinggung C di T dan ada garis lain yang melalui P dan pusat C memotong C pada M dan N. Tunjukkan bahwa (PM)(PN) = PT2.
Penyelesaian: by: sahabat-informasi.com

Kira-kira gambarnya seperti itu, terserah mau meletakkan titik P di mana,
Ingat kembali bahwa garis singgung pada sebuah lingkaran selalu tegak lurus dengan jari-jari lingkaran pada titik singgung itu, berarti segitiga PTC adalah segitiga siku-siku dengan siku-siku di T.
Perhatikan gambar:
Dalam Soal-soal 21-26, cari pusat dan jari-jari lingkaran dengan persamaan yang diberikan (lihat Contoh 3)
















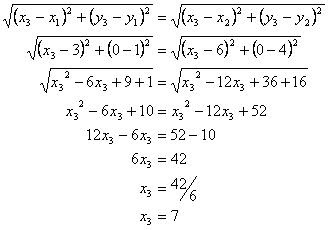














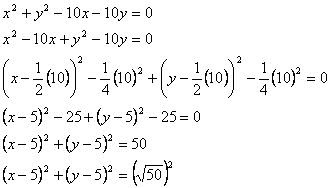


































2 komentar:
ty pembahasannya bang
kepalaku mau pecah
kak soal dan pembahasan tentang limit di buku kalkulus purcell ada gak
Posting Komentar